概率模型

机器学习的目标就是通过使用概率模型来很好的理解得到的数据。 那么由于我们进入了大数据时代，机器学习的用途变得越来越多。 机器学习的初衷是一旦统计模型能够得以建立，那么所有的数据都可以通过模型和其附带的参数进行归纳与总结。如果问题的目标是寻找数据之间的不同，那么这种模型就叫做判别模型 (discriminative model)。如果目标是进一步寻找数据为什么是这个样子，那么这样的模型就叫做生成模型 (generative model)。

当前实际的工程应用还主要集中在数据的检测与分类方面，判别模型有着更实际的作用和人气。 但我个人还是更倾向于寻找事物本质的生成模型。

生成概率模型

生成模型所追求的是数据的全概率模型。因此通过生成模型，我们不仅能够理解数据，而且还可以据此生成模拟数据，甚至可以基于模拟数据对未来进行蒙特卡洛估计。

对于连续实数数据，高斯模型是我们简化数据和解析模型的重要假设。

高斯模型的最大似然估计

我们由易到难，以一维数据为例。

假设我们观测到了一组一维数据\( \mathbf{O} \)，可以想到的最简单的数据模型就是高斯模型。具体来说，就是所有的数据点\( O_i \in \mathbf{O} \) 都被假设成为一个参数后的一维高斯模型的样本。我们知道高斯分布，被它的参数 \( \theta = (\mu, \sigma^2) \)唯一决定。 那么也就是说，我们的目标是寻找最合适的高斯模型参数\( \hat{\theta} \)能够生成观测数据\( \mathbf{O} \)。

高斯分布作为一个概率模型，它可以度量每一个数据点相对于参数模型之间的可能性。所以我们一旦确定了参数\( \theta \)和观测数据\( O_i \)之后，就可以使用概率密度函数\( p( O_i | \theta) \)来进行度量。由于这个概率度量可以被理解为是一种相似（概率越高，相似度越高），所以这个相对于数据点的概率密度函数\( p( O_i | \theta) \)又可以被表示为相对于参数\( \theta \)的似然函数\( \mathcal{L} (\theta | O_i) \)。

很自然的，一个好的模型参数就是能够最大化的相似观测到的数据。为此我们称这个\(\hat{\theta} \)是一个最大似然估计 (maximum likelihood estimation)，并且这个相似度还可以被度量为\( \mathcal{L} (\hat{\theta} | O_i) \)。

以上是针对单独一个数据观测点\( O_i \)的估计，而实际我们观测的是大数据，即一组观测点 \( \mathbf{O} \)。因此我们需要最大化的是\( \mathcal{L} (\theta | \mathbf{O}) = \prod_i \mathcal{L} (\theta | O_i) \)。

这个时候我们就应该感谢高斯函数的性质了，最大化上面的连乘，可以被重构为最大化对数似然函数的加和。而高斯函数取对数后可以方便的在数学上进行求和。 \[ \arg\max_{\theta} \mathcal{L}' (\theta | \mathbf{O}) = \sum_{i} \log P(O_i | \theta) \] 求解以上的最优化方程无需赘述，其结果就是所谓高斯模型最大似然估计的 Sample Mean 和 Sample Variance。我们可以保证在高斯模型假设成立的情况下，这个估计最大了似然函数。

当然似然函数只是数据与模型之间的一种度量，我们还可以选择其他更加复杂的度量函数。 比如考虑贝叶斯统计的情况下，我们可以引入模型参数\( \theta \)的先验信息，这样我们就可以最大化后验概率（似然函数和先验函数根据贝叶斯公式）。

标普数据举例

我们时常听到股票每日的涨跌是无法预测的，那么是否真的如此呢？

为此我们假设标准普尔500的ETF每日的对数回报服从一个高斯分布。 那么该分布的参数则是已知历史数据后高斯模型的最大似然估计。

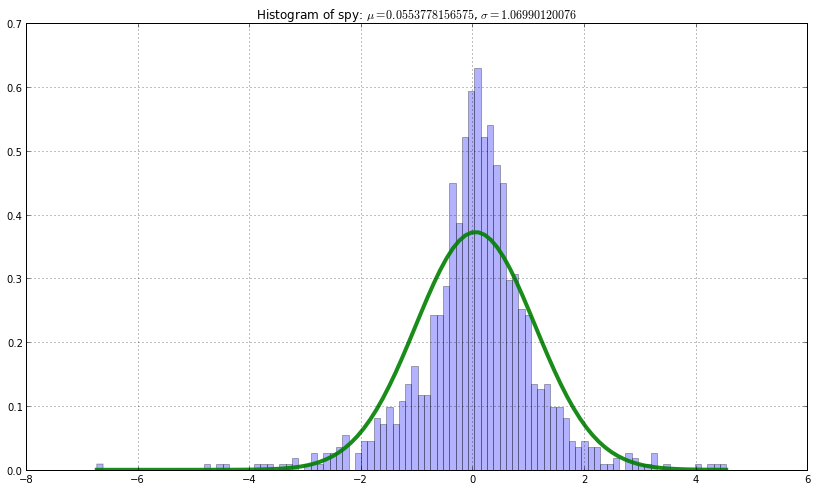
我们用计算得出的高斯模型与真实数据的直方图进行了对比。 首先平均来看，标准普尔有着0.05%的单日正回报率。 其次真实数据分布是长尾，简单的认为股票的单日回报率服从一个高斯分布是不够的。

高斯模型的推广

简单的假设所有的数据都服从单一的高斯模型是仅仅不够的。

首先所有的数据点并非都来自于一个高斯模型，这样我们就需要在模型中考虑多个高斯模型。

其次每一个数据点有可能不是统计独立的，比如在时间序列里，上一时刻和下一时刻的数据往往是有关的。这样我们就需要重新构造一个模型考虑到这种相关性。

针对以上的不同情况，在单独的高斯模型基础之上，我们引入一些新的模型来重新解释数据。

混合高斯模型 Gaussian Mixture

如果我们假设数据是从\( K \)个混合高斯模型产生的， 那么对于任意一个数据点，它与模型的度量可以被进一步简化为其对每一个高斯模型度量的加权平均值。 \[ \mathcal{L} (\theta, w | O_i) = \sum_{k}^K w_k P(O_i | \theta_k)\\ \arg\max_{\theta, w} \mathcal{L} (\theta | \mathbf{O}) = \prod_{i} \mathcal{L} (\theta, w | O_i)\\ \arg\max_{\theta, w} \log \mathcal{L} (\theta | \mathbf{O}) = \sum_i \log \mathcal{L} (\theta, w | O_i) \] 这个模型虽好，但由于我们要对求和求对数，所以虽然还是高斯函数，但是无法求出最优解析解。 我们退一步去寻找局部最优解，则可以使用最大期望 (Expectation-maximization)的办法，迭代的寻找最优值。具体的细节不再赘述。

标普数据举例

对同样的标普数据，我们使用K为3的混合模型进行参数估计。

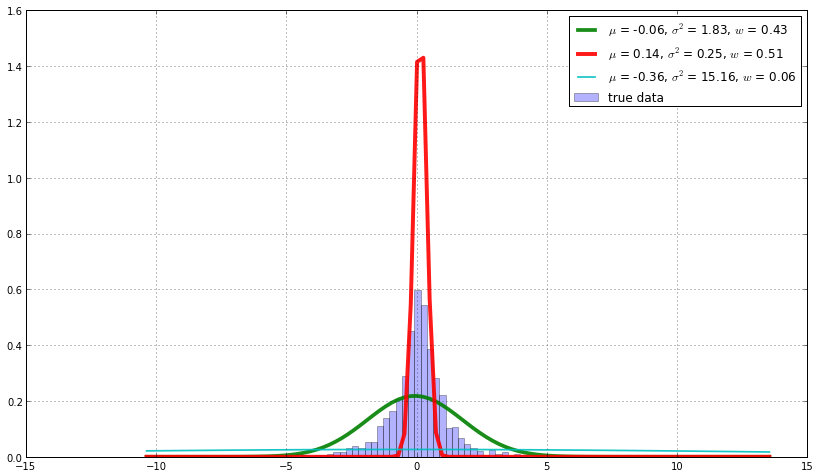
从图中可以看到，多个高斯模型通过进行互补来逼近真实的长尾分布。 其中主分量是由日回报为0.14%和-0.06%的两个高斯模型构成。

高斯马尔科夫模型 Gaussian Markov

在多个高斯模型的基础之上，我们进一步认为多个高斯模型之间并不是独立的。 每一个单独的高斯模型的激活也不是均匀分布的。 这个假设听起来有一定道理，但是引入了太多的不确定性。 为此我们需要简化成，多个不同的高斯模型的激活只与上一个模型有关，换句话说模型与除上一个时刻的模型以外是条件独立的。那么这样的关系就是典型的一阶马尔科夫模型。

我们考虑数据有先后关系，使用\( t \)来描述。这样观测点集\( \mathbf{O} \)从此有了顺序，我们按照\( t \)整理得到\( \mathbf{O} = {O_1, O_2, \ldots, O_n} \)。

和混合高斯模型相比，新的模型不仅要考虑到了\( O_t \)，还需要考虑\( O_{t-1} \)。 不同的高斯模型之间，不再是仅以\( \mathbf{w} \)决定的简单的独立加权关系，而是较为复杂的转移矩阵\( \pi \)。

实际的公式与求解不再赘述，与混合高斯模型一样，隐含马尔科夫模型 (HMM)也没有解析解。 需要使用EM的办法迭代寻找局部最优解。

标普数据举例

标普的日回报数据是典型的时间序列，据此我们考虑其一阶时间关系。

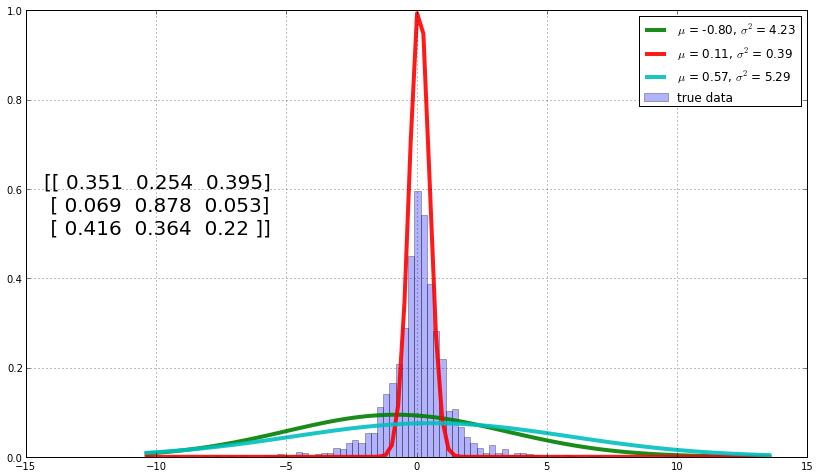
从图中可以看到，真实数据由三个相互转换的高斯模型来逼近。 模型1，2和3的日回报率分别是-0.80%，0.11%和0.57%，这大致对应着跌，几乎不变和涨三个不同的状态。

因为存在一阶时间关系，我们有三个模型的转移状态概率，据此可以对标普的日回报进行简单预测。 如果今天的回报进入状态2，则明日依然是状态2的概率高达87%。 而如果今天的回报状态是1和3，则明日进入3个状态的概率大致相同。

卡尔曼滤波器 Kalman filter

马尔科夫模型假设不同高斯模型之间存在着一阶的相关性，而\( K \)个模型之间有着一阶的马尔科夫关系。 由于每一个模型由参数\( \theta_k \)唯一决定，那么实向量\( \theta_k \)在一些应用中有着线性变换的关系即马尔科夫过程。 在这种特殊情况下，模型随着时间做高斯线性变换，那么这个随着时间迭代的优化系统被就称之为卡尔曼滤波器。

题外话：“如果系统的状态模型变换不是线性高斯的，则需要更为复杂的粒子滤波器 (Particle filter) 模型。大致的思想是，即使使用EM算法对参数进行逼近，其每一个子步骤由于都是非高斯的，也无法直接解析计算，需要使用蒙特卡洛产生模拟点，并通过计算模拟点的统计量估计参数。”

由于股票的回报率以及其模型的变换往往不是线性的，所以不再使用标普的数据作例子。